Logika i instrukcje warunkowe
Informacje o module:
- Poziom: Podstawowy
- Profil: Dla wszystkich
Czy komputery się mylą?
Często słyszymy o spektakularnych skutkach błędów oprogramowania. Ostatnio mieliśmy w USA kilka wypadków (w tym jeden śmiertelny) spowodowanych przez programy, którym powierzono prowadzenie samochodów bez kierowcy. Bardziej poprawne jest mówienie o błędach programistów – ostatnio raczej o tym, że nie wszystko zostało w programach uwzględnione. Tak było z samochodem, który „nie zobaczył” naczepy, gdyż miała ona stosunkowo duży prześwit pod spodem, a czujniki były oślepione słońcem. Pomijając awarie sprzętowe, komputery działają bezbłędnie!
W pewnym sensie bezbłędne są także programy – inaczej nie przeszłyby przez kompilację. Nie zawsze robią to czego oczekujemy, ale zawsze to co programista zakodował!
Co zatem znaczy, że program jest poprawny?
Dla programisty znaczy to, że:
- Jest napisany zgodnie z regułami określonymi w specyfikacji języka programowania.
- Jest sensowny – czyli inaczej mówiąc napisany precyzyjnie. Nie odwołuje się do nie istniejących danych i kończy swe działanie w rozsądnym czasie.
- Wykonuje dokładnie to, co zamierzył programista (lub zleceniodawca).
Ten ostatni punkt – choć najważniejszy – jest przedmiotem zainteresowania inżynierii oprogramowania.
Punkt pierwszy – czyli kodowanie zgodnie z regułami wymuszają na nas translatory (gdy translacja prowadzi do uzyskani kodu maszynowego, translator nazywamy kompilatorem) lub interpretery (czyli translatory uruchamiane w procesie uruchamiania programu).
Pisanie programów sensownych jest natomiast sztuką inżynierską, której musimy się nauczyć.
Program musi bardzo precyzyjnie opisać działanie komputera. To jest zasadnicza różnica wobec posługiwania si językiem naturalnym (w naszym wypadku polskim). Gdy komuś powiemy, że coś jedzie drogą – to każdy się domyśli, że chodzi o pojazd, a w razie potrzeby – sprawdzi co dokładnie. Gdybyśmy taką nieokreśloną instrukcję zawarli w komputerze – w najlepszym razie dostaniemy komunikat w rodzaju „nie rozumiem”.
Poprawne wypowiedzi dotyczące rzeczywistości muszą mówić o tym co jest naprawdę. Czyli poprawny = prawdziwy. W komputerze „poprawność” oznacza, że program działa zawsze tak samo i na dodatek zgodnie ze specyfikacją.
Brak sprzeczności oraz determinizm w działaniu wynikają z samej istoty działania komputera. Determinizm oznacza, że dla danych warunków efekt zawsze będzie taki sam. Jeśli komputer nie ulega awarii – to w tym sensie jego obliczenia zawsze są prawdziwe. Jednak źle napisany program może sprawić, że „dane warunki” nie zawsze będą takie same – w szczególności mogą odbiegać od założeń. Jeśli na przykład program odwołuje się do zmiennej, której wartości wcześniej nie zainicjował – to otrzymana wartość zależy od historii działania komputera i można ja uznać za losową.
Także sprzeczność jest łatwa do wprowadzenia. Weźmy na przykład fragment programu:
jeśli a>=b to napisz(‘a>b’); jeśli a<=b to napisz(‘a<b’);
Program dla a=b napisze, że a>b i a<b równocześnie. Takie błędy (użycie złego znaku porównania) są bardzo często spotykane.
Jak to ma się do tezy, że w komputerze nie może być sprzeczności? Na poziomie kodu maszynowego nie ma żadnej sprzeczności w działaniu. Komputer wypisuje w określonej sytuacji określony wynik on nawet „nie wie”, że drukowany napis ‘a>b’ zawiera wyrażenie logiczne (dla niego to tylko dana – ciąg bitów). Warto w tym miejscu przypomnieć rozróżnienie języka i metajęzyka (moduł 2 w pierwszej części).
Najczęstszym jednak źródłem uzyskiwania nieoczekiwanych wyników są błędne dane, jakie są przedmiotem obliczeń. Informatycy sformułowali nawet sentencję określającą tą sytuację:
To określenie dotyczy także programów, które są daną wejściową dla translatorów. Chcąc uzyskać poprawny program, musimy samemu zachować precyzje i stosować zasady logiki.
Problem złożoności
Pamięć komputera zawiera bity. Co to dokładnie znaczy? Bit to najmniejsza porcja informacji – wybór jednego z dwóch elementów. Najczęściej wybieramy między zerem a jedynką (tak jest w komputerach). Odpowiada to oczywiście wartościom fałsz (zero) i prawda (jeden) w logice.
Zaprojektujmy sobie najprostszy komputer, który komputer, który liczy jedynie sumy wyłączne (XOR) z sygnałów podanych na wejściu. Suma wyłączna (A XOR B) czyli inaczej „albo albo” daje na wynik prawdę, gdy prawda jest na wejściu A albo na wyjściu B, ale nie na obu. Natomiast iloczyn (A i B, A AND B) daje prawdę, gdy zarówno A jak i B mają wartość prawda.
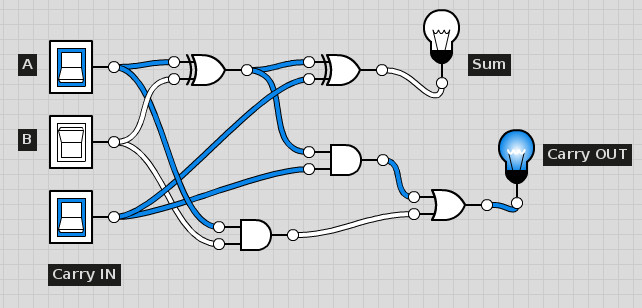
Odpowiedni przykład funkcji przejścia można przetestować na stronie http://logic.ly/demo/ (trzeba wybrać przykład opisany jako „1-Bit Full Adder”):
Zmieniając przyciski A i B możemy obserwować co dzieje się na wyjściu – czy pali się lampka Sum. W tym przykładzie mamy dodatkowo sygnały przeniesienia (Carry IN na wejściu i Carry OUT na wyjściu). Umożliwiają one połączenie kaskadowo tych sumatorów dla uzyskania sumy z więcej niż dwóch wejść (wynik Carry OUT łączymy do Carry IN z następnej pary).
Żeby można było mówić o komputerze, a nie tylko o układzie elektronicznym, poszczególnym elementom wejścia i wyjścia muszą odpowiadać komórki pamięci, a wynik obliczeń powinien zostać zapisany w komórkach odpowiadających wyjściu w takt zegara odliczającego instrukcje.
W tak prostym przykładzie mamy 5 jednobitowych komórek pamięci i 5 układów elektronicznych (bramek logicznych).
Jaka zatem powinna być złożoność komputera przetwarzającego informację o złożoności liczonej w milionach bitów? Ogromna. Prostszym jest pytanie postawione od drugiej strony: ile maksymalnie bitów zmieniają za jednym razem współczesne komputery? Jeśli słyszymy, że mamy procesor 64-bitowy, to oznacza właśnie tyle, że naraz może odczytać lub zapisać 64 bity. Większą ilość komórek pamięci można zmienić w wielu kolejnych taktach zegara. Niektóre obliczenia są tak złożone, że takie sekwencyjne (krok po kroku) obliczenia nie skończyłyby się nawet za tysiąc lat.
Instrukcje warunkowe
Nie tylko ograniczenia sprzętowe (budowa komputera) sprawiają, że z zasady obliczenia w komputerze odbywają się w sposób sekwencyjny: instrukcja po instrukcji. Człowiek także nie jest w stanie myśleć równolegle (podobno kobiety mają większą podzielność uwagi – ale to zrównoleglenie też nie jest wielkie ;-)).
Jakie instrukcje są nam potrzebne, aby zapisać dowolny proces obliczeniowy? Okazuje się, że wyliczaniem wartości wyrażeń arytmetycznych i logicznych potrzebujemy jedynie instrukcji warunkowych (wykonaj coś pod warunkiem) oraz mechanizmu pozwalającego przeglądać zbiór danych. Takim mechanizmem są tak zwane pętle (choć może to też być też tak zwany mechanizm rezolucji – dla bardzo zaawansowanych: https://pl.wikipedia.org/wiki/Rezolucja_(matematyka), https://pl.wikipedia.org/wiki/Prolog_(j%C4%99zyk_programowania)).
Dla przykładu z sumą wyłączną ciąg instrukcji wyliczającej XOR dla 4 danych wejściowych (A,B,C,D) może wyglądać następująco:
jeżeli (A XOR B) to
jeżeli (C XOR D) to
napisz(‘prawda’);
Proszę zwrócić uwagę na tak zwane wcięcia (odstępy z lewej) – powszechnie stosowane dla większej czytelności programów.
Instrukcje warunkowe są podstawą programowania. Można wykazać, że do takiego zbioru instrukcji daje się sprowadzić wszystkie wyrażenia logiczne! Istnieją języki programowania, które składają się wyłącznie z takich warunkowych instrukcji. Nie ma zaś żadnego bardziej złożonego języka programowania, który nie zawierałby takich instrukcji.
Logiczne myślenie – uwaga metodologiczna:
Zbudowanie przez Boole'a rachunku logicznego na wzór algebry było bardzo ważnym odkryciem. Wpłynęło jednak na to, że najbardziej naturalną umiejętność człowieka postrzegamy dzisiaj jako rzecz trudną. Nauki logiki nie powinno się zaczynać od operowania na symbolach i wyrażeniach, ale od prostych pytań w rodzaju: co zrobić, aby osiągnąć jakiś efekt. To mogą być proste historie (na przykład: aby włączyć notebooka trzeba podnieść klapę i nacisnąć przycisk, ale jeśli bateria jest rozładowana, musimy włączyć go dodatkowo do prądu). Po dojściu do końca w analizie postawionego problemu, można zapisać działania w odpowiedniej kolejności, uzyskując prosty algorytm.
Zadanie: Napisać program w postaci instrukcji warunkowych JEŚLI, wyliczający ilość dni dowolnego miesiąca w dowolnym roku
html:
<form>
rok= <input id="rok" type=text value="2016"><br />
miesiąc= <input id="mies" type=text value="01"><br />
<input type="button" onclick="javascript:licz()" value="licz"/><br >
dni= <input id='dni' type=text value="00" readonly/><br />
</form>
Javascript:
function licz(){
rok=document.getElementById('rok').value;
mies=document.getElementById('mies').value;
var dni='31';
if (mies=='02') {
dni='28';
if (rok==2016) { dni='29'; }
}
if (mies=='04') { dni='30'; }
if (mies=='06') { dni='30'; }
if (mies=='09') { dni='30'; }
if (mies=='01') { dni='30'; }
document.getElementById('dni').value=dni;
}
Implementacja w JavaScript: http://codepen.io/pen/ lub https://jsfiddle.net/ lub http://jsbin.com/
(dla innych języków: https://repl.it).
Zadanie domowe: zrobić program dla dowolnych lat.
Podsumowanie
- Komputery działają w sposób deterministyczny – czyli dla danych warunków efekt zawsze będzie taki sam.
- Poprawność działania komputera nie gwarantuje tego, że obliczenia są wykonywane zgodnie z naszymi oczekiwaniami. Aby to zapewnić, program dostarczany do translatora musi być napisany zgodnie z zasadami logiki.
- Teoretycznie do tworzenia dowolnych programów wystarczy, by w języku programowania był zawarty interpreter wyrażeń arytmetycznych i logicznych, instrukcje warunkowe i mechanizm przeglądania zbiorów danych.