Elementy językozastwa dla programistów
| Moduł: Elementy językozawstwa dla programistów |
| Poziom: Zaawanowany |
| Profil: Dla profesjonalistów |
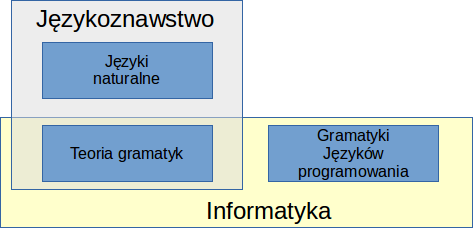
Każda wypowiedź ma swoją strukturę, którą określamy terminem „syntaktyka” lub składnia, oraz swoje znaczenie określane terminem „semantyka”. Obydwie te dziedziny są przedmiotem zainteresowania informatyki – ale ich znaczenie jest zupełnie różne. Semantyka to przedmiot badania sztucznej inteligencji (komunikacja w języku naturalnym, przetwarzanie wiedzy) oraz filozofii informatyki. Badania syntaktyki zostały natomiast wykorzystywane w rozwoju języków programowania.
Analizy językoznawców wykazały, że zdania dowolnego języka daje się opisać w postaci reguł budowania złożonych wypowiedzi z prostszych struktur. Proces generacji zdań nazywa się też procesem „wywodu”.
Przykład:
Powstała struktura ma kształt odwróconego drzewa. Dlatego nazywa się ją „drzewem wywodu”.
Gramatyka struktur frazowych
Językoznawca Noam Chomsky stworzył teorię zwaną gramatyką generatywną (lub gramatyką struktur frazowych) opisującą ten proces generacji (dla zdań w formie podstawowej). Informatycy podążyli dalej w tym kierunku tworząc sztuczne języki i automaty je analizujące (translatory). Podstawą była formalizacja teorii gramatyk, którą w zarysie przedstawiono poniżej.
Gramatyka składa się z: * zbioru symboli terminalnych T (symboli wchodzących w skład wygenerowanych zdań);
- zbioru symboli nieterminalnych N (zbiór symboli pomocniczych służących do przeprowadzenia generacji, oznacza się je często przez ujęcie w nawiasy ostre <...> = zob. NotacjaBNF);
- symbolu początkowego S (wyróżniony symbol nieterminalny od którego rozpoczyna się wywód);
- reguł wywodu pozwalających na zastępowanie symboli nieterminalnych przez ciągi symboli terminalnych i nieterminalnych aż do otrzymania samych symboli terminalnych;
Przykład:
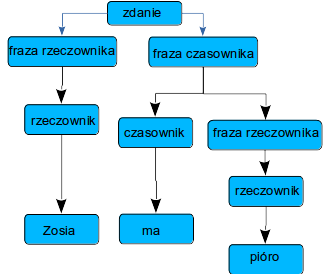
Dla zdania na powyższym obrazku można zaproponować gramatykę:
T = { Jan, Zosia, trzyma, ma, czapka, pióro }
N = { <zdanie>, <fraza rzeczownika>, <fraza czasownika>, <rzeczownik>, <czasownik> }
S = <zdanie>
reguły wywodu ( ::= oznacza operację zastępowania):
(1) <zdanie> ::= <fraza rzeczownika><fraza czasownika>
(2) <fraza rzeczownika> ::= <rzeczownik>
(3) <fraza czasownika> ::= <czasownik><fraza rzeczownika>
(4) <rzeczownik> ::= Jan | Zosia | czapka | pióro (5) <czasownik> ::= trzyma | ma
Znak '|' oznacza alternatywę - np. można użyć reguły <czasownik> ::= trzyma lub <czasownik> ::= ma
Wywód przykładowego zdania ( w nawiasach podano numery użytych reguł ):
S -(1)-> <fraza rzeczownika> <fraza czasownika> -(2)-> <rzeczownik><fraza czasownika> -(4)-> Zosia <fraza czasownika> -(3)-> Zosia <czasownik> <fraza rzeczownika> -(5)-> Zosia ma <fraza rzeczownika> -(2)-> Zosia ma <rzeczownik> -(4)-> Zosia ma pióro
Powyższy wywód można przedstawić w postaci drzewo wywodu, pokazanego na powyższym rysunku. Przy analizie drzewo wywodu nazywane jest też drzewem rozkładu (w jaki sposób zdanie rozkładamy na jego reprezentację). Drzewo to służy następnie wygenerowaniu kodu programu - wykonywanego przez komputer.
Liście tego drzewa stanowią symbole terminalne. Każde poddrzewo drzewa wywodu nazywa się frazą. Ze względu na typ użytych reguł wywodu, gramatyki dzieli się na:
- regularne: wszystkie reguły są w postaci A ::= aB, lub A ::= a, gdzie A, B - oznaczają symbole nieterminalne, a - symbol terminalny;
- bezkontekstowe: daje się sprowadzić do zbioru takich reguł, że po lewej stronie każdej reguły wywodu znajduje się pojedynczy symbol nieterminalny (zob. postać normalna Greibach);
- kontekstowe: reguły wywodu mogą być dowolnej postaci;
Mniej formalnie można powiedzieć, że gramatyka bezkontekstowa to taka, że przy analizie wypowiedzi można na podstawie wczytanych symboli dokładnie ustalić którą regułę wywodu należy zastosować.
Zależnie od gramatyki jaka jest konieczna do wygenerowania zdań języka mówimy o językach regularnych, bezkontekstowych i kontekstowych.
Gramatyki regularne opisują między innymi budowę poszczególnych elementów używanych w językach programowania komputerów (identyfikatory, liczby, słowa kluczowe). Instrukcje języków takich jak Pascal pochodzą z języków bezkontekstowych. W praktyce analiza języków programowania odbywa się dwustopniowo. Najpierw tzw. skaner wydziela z wejściowego łańcucha znaków 'tokeny', czyli wspomniane wcześniej proste elementy znaczeniowe. Później 'parser' analizuje ciąg tokenów tworząc z nich instrukcje języka. Skaner jest zazwyczaj automatem implementującym gramatykę regularną.
Języki regularne. Automaty.
Tokeny (liczby, napisy, słowa kluczowe), na które skaner dzieli przetwarzany ciąg znaków mają strukturę, którą można opisać gramatyką języków regularnych. Najbardziej naturalną metodą zapisywania konstrukcji języka regularnego są wyrażenia regularne. Użycie znaku * w tym wyrażeniu oznacza powtórzenie >=0 ilość razy poprzedzającego go symbolu.
Przykład:
| wyrażenie | przykłady użycia |
| xy*z | xyyz, xz, xyyyz |
| (xy)*z* | xyxyzzzz, xyzzzz |
Analizę języków regularnych wygodnie jest opisywać (a niekiedy także implementować) jako działanie automatów skończenie-stanowych. Automat skończenie-stanowy to zbiór stanów połączonych ze sobą przy pomocy etykietowanych symbolami łuków (lub innych połączeń). Wyróżniany jest jeden stan jako stan początkowy i zbiór stanów końcowych.
Zadaniem automatu jest analiza ciągu znaków. Jego działanie polega na przechodzeniu od stanu do stanu począwszy od stanu początkowego. Przejście jest możliwe, o ile analizowany symbol (znak) jest identyczny z definicją (etykietą) przejścia. Po przejściu pobierany jest do analizy następny symbol (znak). Jeśli po przetworzeniu całego ciągu znaków automat znajdzie się w stanie końcowym, ciąg należy do języka regularnego (jest akceptowalny przez automat), a stan końcowy wskazuje na to, co ciąg ten oznacza.
Przykład:
Automat akceptujący ciąg symboli: a, ab*, lub ab*c oznaczenia:* okrąg oznacza stan początkowy
- prostokąty z okrągłymi rogami (niebieskie) - oznaczają stany końcowe
- prostokąty(pomarańczowe) - pozostałe stany
Uzupełnieniem tego niniejszego są programy z repozytorium https://github.com/galicea/eduprog. W podkatalogu lang można znaleźć program autogram, który tworzy automat na podstawie wyrażeń regularnych. Wywołanie dla powyższego przykładu:
autogram -a -i "a(&b&)@c"
W wyniku analizy otrzymujemy tabelkę przejść:
| | a | b | c |
| 1 | 2| 0| 0 |
| 2 | 0| 2| 3 |
| 3 | 0| 0| 0 |
W wierszach są zawarte stany automatu, a w kolumnach symbole wyrażenia. Kolumny opisują do którego stanu automat przejdzie po wczytaniu symbolu. Na przykład w stanie 2 symbol b powoduje pozostanie w tym samym stanie, a symbol c - przejście do końcowego stanu 3 (gdzie już nic nie można przyjąć).
Gramatyki bezkontekstowe
Aby utworzyć drzewo wywodu dla dowolnego zdania zbudowanego w oparciu o gramatykę należałoby po kolei próbować zastosować wszystkie produkcje (poddrzewa), wracając w razie niepowodzenia do wcześniejszego stadium analizy. Ten sposób analizy (analiza z powrotami) jest jednak bardzo nieefektywny. W praktyce na gramatyki bezkontekstowe nakłada się dodatkowe ograniczenia pozwalające jednoznacznie wskazać którą produkcję należy wybrać na podstawie: * dotychczasowego przebiegu analizy (stanu w którym znajduje się analizator (automat));
- k symboli na wejściu (w praktyce prawie zawsze k=1);
Analiza lewostronna (wywód lewostronny) polega na tym, że czytamy kolejne symbole i na tej podstawie decydujemy jaką regułę zastosować. Potrzebna do tego gramatyka jest określana mianem LL(1) – dla podkreślenia, że chodzi o 1 symbol z lewej strony drzewa wywodu. Taką gramatykę zastosowano w języku Pascal. Drugą metodą analizy jest analiza prawostronna. Polega ona na tym, że wczytujemy kolejne symbole aż do chwili, gdy skompletujemy wszystkie symbole potrzebne do zastosowania reguły wywodu. Decyduje o tym zawsze ostatni wczytany symbol – czyli symbol z prawej strony drzewa wywodu. Stąd określenie LR(1).
Gramatyki LL(1)
Gramatyka LL(1) ma tą własność, że każdą produkcję można zidentyfikować na podstawie pierwszego z lewej symbolu po prawej jej stronie. Gramatyki tego typu są najczęściej stosowane przy 'ręcznym' konstruowaniu analizatora. Stosuje się przy tym analizę rekurencyjną. Polega ona na tym, że dla każdej produkcji tworzy się procedurę ją analizującą. Procedury te identyfikują i wywołują odpowiednie procedury dla zanalizowania podfrazy. Dokładny opis tej metody analizy można znaleźć w podręczniku N.Wirtha [2].
Poniżej prosty przykład kalkulatora wyrażeń w języku Python, który zawiera analizator LL(1). W przykładzie założono, że liczby są dodatnie jednocyfrowe, a dostępne działania to tylko mnożenie i dodawanie. Dzięki temu skaner (next_token) to tylko pobieranie kolejnego znaku (znak dolara oznacza koniec wejścia a wykrzyknik błąd). Proszę zauważyć, że wystarczy zawsze sprawdzić jaki jest kolejny token, by zdecydować o następnym kroku analizy. Ta stosunkowo prosta zasada sprawia, że analizatory LL(1) można zaimplementować ‘ręcznie’ - bez programów wspierających – takich jak Yacc czy Bison.
class calculator():
source=[]
digits = ('0','1','2','3','4','5','6','7','8','9')
result=0
token='!'
def next_token(self):
if len(self.source)==0:
self.token='$'
else:
self.token=self.source[0]
del self.source[0]
def factor(self): # czynnik
self.result=0
if self.token=='(':
self.next_token()
self.expr()
if self.token != ')':
self.token='!'
else:
self.next_token()
elif self.token in self.digits:
self.result=int(self.token)
self.next_token()
def term(self): # skladnik
self.factor()
mem=self.result
while self.token=='*':
self.next_token()
self.factor()
mem=mem*self.result
self.result=mem
def expr(self):
self.result=0
self.term()
mem=self.result
while (self.token=='+'):
self.next_token()
self.term()
mem=mem+self.result
self.result=mem
def calc(self,expression):
self.source=list(expression)
self.next_token()
self.expr()
if self.token=='$':
return self.result
else:
return None
Przykładowe użycie kalkulatora:
c=calculator()
res=c.calc('4*(2+3)')
if res != None:
print(res)
else:
print('error')
Gramatyki LR(1)
W przeciwieństwie do poprzedniej, tą gramatykę stosuje się najczęściej przy użyciu generatorów przy pomocy których konstruuje się analizator. Pouczającym może być analiza takiego generatora. W repozytorium https://github.com/galicea/eduprog, w podkatalogu lang znajduje się moduł u_makerl1 i program autogram wykorzystujący ten moduł generatora. Oprogramowanie jest napisane w języku Pascal (z polskimi komentarzami). Może więc być łatwiejsze w analizie (zwłaszcza, że poniżej podano szczegółowe objaśnienie algorytmu), niż rozbudowane generatory wspomniane wcześniej.
Metoda analizy
Analizator jest automatem ze stosem. Oznacza to, że zawiera on pamięć w postaci stosu do której może dopisywać dane dotyczące aktualnego stanu (wkładanie na stos). Możliwe jest także odczytywanie danych w kolejności odwrotnej do tej w jakiej były zapisywane (zdejmowanie ze stosu). Automat pobiera kolejne symbole, wkłada je na stos i zmienia swój stan. Bieżący stan automatu jest zapisywany na stosie wraz z symbolem. Stan automatu opisuje całą zawartość stosu. Jeśli stan ten wskazuje, że na stosie jest pełna fraza - następuje redukcja. Polega ona na zdjęciu ze stosu symboli składających się na tą frazę i zastąpieniu ich symbolem nieterminalnym będący lewą stroną produkcji dającej taką frazę.
Dzięki pamiętaniu stanu na stosie - po redukcji można ustalić nowy stan automatu. Stan zapisany na wierzchołku stosu opisuje bowiem całą jego zawartość i możemy ustalić jaki stan powstanie po dodaniu nowego symbolu.
Analiza kończy się poprawnie, gdy pojawi się symbol sygnalizujący koniec danych, a na stosie znajduje się symbol początkowy gramatyki.
Gramatyka dla takiej metody analizy musi spełniać jeden warunek: prawe części żadnych dwóch produkcji nie mogą być jednakowe (trzeba wiedzieć w oparciu o którą produkcję dokonać analizy).
Ponieważ w trakcie analizy badamy zawsze jeden - ostatni z prawej symbol wywodu - metoda ta, oraz gramatyka noszą nazwę LR(1).
Algorytm tworzenia automatu LR(1)
1/ Ułożyć gramatykę LR(1) języka. Ponumerować wszystkie produkcje.
2/ Spisać wszystkie możliwe stany automatu. Jeśli dowolną produkcję można przedstawić w postaci X::=PS, to P jest jednym z możliwych stanów automatu.
3/ Utworzyć funkcję zmiany stanu stosu przy akceptacji tokenów. Rozróżniamy dwa rodzaje operacji: przesunięcie i redukcja. Przesunięcie polega na dodaniu tokenu na stos. Po przesunięciu pobierany jest następny token. Redukcja polega na zdjęciu ze stosu pełnej frazy.
PRZESUNIĘCIE:
1) Jeśli istnieją stany stosu PQ i Qt, to dla tokenu t istnieje przejście od stanu PQ do stanu Qt; (oznacza to przejście do analizy podfrazy będącej bardziej z prawej strony).
2) Jeśli nie zachodzi przypadek 1 - badamy zamiast t wszystkie symbole z których t można wyprowadzić lewostronnie. Oznacza to że jeśli istnieją stany PQ i z QR, oraz z R można wyprowadzić lewostronnie t, to dla tokenu t istnieje przejście od stanu PQ do stanu t;
REDUKCJA:
Dla każdego stanu stosu PQ szukamy najdłuższego łańcucha Q spełniającego warunki: - istnieje produkcja (reguła gramatyczna) r, dla której Q stanowi prawą stronę; - istnieje stan Pl(r), gdzie l(r) oznacza lewą stronę produkcji r; Redukcja r jest wykonywana w sytuacji, gdy przy stanie PQ pojawi się token, dl którego nie można dokonać przesunięcia.# Utworzyć funkcję przejścia do nowego stanu przy redukcji. Jeśli po dołączeniu do stanu ze szczytu stosu lewej strony produkcji r otrzymamy poprawny stan - jest to stan do którego następuje przejście automatu. Jeśli taki stan nie istnieje - następuje próba zanalizowania nowej frazy. Ustalany jest nowy stan opisujący lewą stronę użytej produkcji.
4/ Zbudować automat działający wg. zasady:
repeat
PobierzNastępnySymbol;
if symbol=znacznikKońcaDanych i na stosie znajduje się symbol początkowy then
koniec
else if dla danego tokenu, oraz aktualnego stanu stosu
istnieje przejście zgodne z funkcja przejścia (pkt. 3) then
włóż symbol na stos z zaznaczeniem nowego stanu
else if istnieje produkcja której prawa strona jest zawarta aktualnie na stosie then
wykonaj redukcję, zmieniając stan na wskazany przez funkcję przejścia zbudowaną w pkt. 4
else
wystapił błąd
until błąd lub koniec;
Szczegółowy opis gramatyk LR(1) można znaleźć w pracy [1].
Przykład
Programem autogram, który zawiera opisany powyżej generator stworzono automat analizujący proste wyrażenia arytmetyczne:
gramatyka (plik gram.lr1):
gramatyka (plik gram.lr1): stany:
1: <Z> ::= <W> 1 : <W>
2: <W> ::= <W> + <A> 2 : <W>+
3: <W> ::= <W> - <A> 3 : <W>+<A>
4: <W> ::= <A> 4 : <W>-
5: <A> ::= <A> * <A> 5 : <W>-<A>
6: <A> ::= <A> / <A> 6 : <A>
7: <A> ::= <B> 7 : <A>*
8: <B> ::= + <C> 8 : <A>*<A>
9: <B> ::= - <C> 9 : <A>/
10: <B> ::= <C> 10 : <A>/<A>
11: <C> ::= ( <W> ) 11 : <B>
12 : <C> ::= NUM 12 : +
13 : +<C>
14 : -
15 : -<C>
16 : <C>
17 : (
18 : (<W>
19 : (<W>)
20 : NUM
Fragmenty tablic sterujących działaniem automatu:
analiza:
| tokeny
stan: | + - * / ( NUM EOIN
------+-------------------------------------------
0 | 12 14 17 20
1 | 2 4
2 | 12 14 17 20
3 | -2 -2 7 9 -2 -2 -2
liczbami dodatnimi oznaczono nowe stany przy przesunięciu, a ujemnymi numery produkcji użytych do redukcji.
EOI = znacznik końca danych
nowe stany po dokonaniu redukcji:
numer | stan
produkcji | 1 2 3 ...... 16 17 18
----------+--------------------------------------
2 | 1 1 1 1 18 1
Zauważ że generator tworzy pewną nadmiarowość. Wynik jego działania można poprawić usuwając dane dotyczące stanów przez które automat nie powinien przechodzić (na przykład w stanie 3 nie może pojawić się symbol '('). Ten automat wykonuje działania tak długo jak to jest możliwe, zamiast zatrzymywać się przy pierwszej nieprawidłowości.
Na podstawie tego automatu stworzono moduł kalkulatora KALK_LR1.PAS. Dla porównania analogiczny kalkulator zbudowano w oparciu o gramatykę LL(1): KALK_LL1.PAS
Bibliografia
- W.M. Waite, G. Goos "Konstrukcja kompilatorów"
- N. Wirth "Algorytmy+struktury danych = programy".