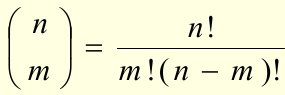Algorytm Simplex
Algorytm Simplex
Algorytm Simplex jest fascynujący z wielu względów. Począwszy od jego twórcy (to on jest tym studentem z anegdoty, który rozwiązał bardzo trudny problem, sądząc, że to zadanie domowe [1]), a skończywszy na współczesnych opisach algorytmu. Co w nich jest fascynującego? Zanim przejdziesz dalej – spróbuj znaleźć w internecie jakiś opis i zrozumieć na jego podstawie, jak ten algorytm działa i dlaczego. Wspomniane opis można z grubsza podzielić na dwie grupy: opis „techniczny” wyjaśnia jakie działania wykonać na danych, aby osiągnąć wynik. Opis teoretyczny zaś wyjaśnia proste zasady, które Simplex wykorzystuje w taki sposób, że bez studiowania algebry wyższej nie jesteś w stanie tego pojąć. Ewidentnie brakuje informacji, które pozwoliłyby nie tylko używać algorytmu, albo pisać naukowe dzieła na jego temat, ale po prostu go zrozumieć. Mam nadzieję, że poniższy tekst wypełni ten brak.
Problem programowania liniowego
Mamy zbiór warunków (ograniczeń) określonych przez nierówności liniowe oraz funkcję celu, zdefiniowaną także w postaci równania liniowego. Chcemy znaleźć rozwiązanie spełniające warunki ograniczeń i maksymalizujące (lub minimalizujące) funkcję celu – definiowaną także jako funkcja liniowa.
Na przykład produkujemy kosmetyki p1 i p2, które mają składy (liczone w porcjach):
dla p1: s1*4+s2*3
dla p2: s1*2+s2*3
produkt p1 kosztuje 12 zł, a produkt p2 kosztuje 15zł. Mamy na magazynie 250 porcji składnika s1 i 300 składnika s2.
Powyższe zagadnienie możemy opisać następująco.
Ograniczenia:
x1*4 + x2*2 < 250
x1*3 + x2*6 < 300
Funkcja celu:
x1*12 + x2*15 → max
przy czym x1 i x2>=0
Oczywiście x1 to ilość produktu p1 do wyprodukowania z zapasów magazynowych. Natomiast x2 to ilość produktu p2 do wyprodukowania.
Jest to typowe zagadnienie programowania liniowego.
Stosując algorytm Simplex znaleźć rozwiązanie dla powyższego problemu: x1=50 a x2=25, natomiast zarobek wynosi 975zł. W dalszej części tekstu znajdziesz wyjaśnienie jak to zrobić.
Równania i nierówności liniowe
Zanim przejdziemy do algorytmu Simplex, musimy poznać przynajmniej podstawy rozwiązywania układów równań i nierówności liniowych.
Rozważmy prosty układ równań:
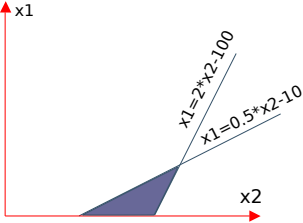
(1) x1=2*x2 - 100
(2) x1=0.5*x2 - 10
rozwiązanie:
0 = 1.5*x2 - 90 | odejmujemy stronami
x2 = 90/1.5 = 60
x1=2*60-100=20
Jeśli zamienimy równania na nierówności – rozwiązaniem będzie trójkąt ograniczony prostymi (zamalowany na niebiesko na powyższym rysunku):
(1) x1>=2*x2 - 100
(2) x1<=0.5*x2 - 10
x1>=0, x2>=0
W zagadnieniu programowania liniowego rozwiązujemy tego typu zbiory nierówności z uwzględnieniem dodatkowo zdefiniowanej funkcji celu, określonej także poprzez równanie liniowe. Nierówności są przy tym interpretowane jako ograniczenia jakie muszą spełniać zmienne występujące w funkcji celu.
Zagadnienie programowania liniowego ma postać standardową, jeśli w ograniczeniach występują wyłącznie równości (=), a wszystkie zmienne przyjmują wartości nie mniejsze niż zero. Zamiana nierówności na równania jest banalnie prosta (wystarczy dodać / odjąć dodatkową zmienną – szczegóły poniżej). Możemy więc poprzestać na rozwiązywaniu równań.
Będziemy przy tym posługiwać się zapisem macierzowym (zobacz https://edu.pjwstk.edu.pl/wyklady/alg/scb/index35.html ):
Ograniczenia:
A*[x] = [b]
[x]>=0
Funkcja celu:
z = f(x) = <[c] * [x]>
Gdzie <> oznacza iloczyn skalarny
W języku Python macierz będzie listą wierszy (też reprezentowanych przez listy).
Dla naszego przykładu:
A = [ [-1,2], [1,-0.5], ]
b = [100, -10]
c = [3,4]
def z(c,x): # Iloczyn skalarny
return sum([c1*x1 for c1,x1 in zip(c,x)])
Zdefiniujmy przykładową funkcję celu:
z = 3*x1+4*x2 → max
Wartości funkcji celu w poszczególnych wierzchołkach (zob. zamalowany obszar na rysunku) będą wynosić:
x1=20, x2=60 (wyliczone powyżej): z=300
x1=0, x2=20: z=20*4=80
x1=0, x2=50: z=50*4=200
maksymalna wartość funkcji celu występuje więc w punkcie (20,60) i wynosi 300
Metoda eliminacji Jordana-Gaussa
Metoda eliminacji Jordana-Gaussa polega na redukcji wszystkich poza jedną niewiadomą każdego wiersza. Operacje wykonujemy na „macierzy uzupełnionej”, w której ostatnia kolumna zawiera wartość równania (wyraz wolny). Przekształcanie polega na mnożeniu wiersza macierzy przez skalar oraz dodawaniu wierszy pomnożonych przez skalar. Takie ‘operacje elementarne’ oczywiście nie zmieniają wartości rozwiązania.
Operacje elementarne:
def mnoz_wiersz(S,wiersz,skalar):
for i,x in enumerate(S[wiersz]):
S[wiersz][i]=x*skalar
def dodaj_wiersz(S,wiersz1,wiersz2,skalar):
for i,x in enumerate(S[wiersz2]):
S[wiersz1][i]=S[wiersz1][i]+x*skalar
Na naszym przykładzie:
S = [[-1, 2, 100],[1, -0.5, - 10],]
dodaj_wiersz(S,0,1,-S[0][0])
Wynik:
S=[ [0, 1.5, 90], [1, -0.5, -10]]
Teraz eliminacja elementów <>0 w kolumnie 1:
mnoz_wiersz(S,0,1/S[0][1])
dodaj_wiersz(S,1,0,-S[1][1])
Najpierw podzieliliśmy wiersz 0 przez drugi jego element (by uzyskać w tym elemencie 1), a następnie odjęliśmy od wiersza drugiego wiersz pierwszy pomnożony przez drugi jego element (by uzyskać w nim 0):
S=[ [0.0, 1.0, 60.0], [1.0, 0.0, 20.0] ]
Ostania kolumna zawiera rozwiązanie!
Postać standardowa problemu
Każde zagadnienie programowania liniowego daje się sprowadzić do postaci standardowej[2]: znaleźć minimum (lub maksimum) funkcji celu z, które równocześnie spełnia zadane ograniczenia (A*x=b).
1. Gdy poszukujemy maksimum a nie minimum funkcji z: wektor c zastępujemy wektorem −c oraz otrzymaną minimalną wartość funkcji mnożymy przez −1.
2. Nierówność ai1 * x1 + ai2 * x2 + . . . + ain * xn <= bi
można sprowadzić do równania poprzez wprowadzenie dodatkowej zmiennej xn+1:
ai1 * x1 + ai2 * x2 + . . . + ain * xn + xn+1 = bi
Podobnie w przypadku, gdy w miejsce znaku mniejszości mamy znak większości. Musimy wprowadzić tyle dodatkowych zmiennych, ile mamy nierówności!
Zmienne te nazywamy „zmiennymi luzu”, albo „swobodnymi” (ile dzieli wynik od ekstremum).
3. Gdy zmienne x nie spełniają ograniczenia (xi>0), korzystamy z faktu, że każda liczba rzeczywista może być przedstawiona jako różnica liczb nieujemnych. Wprowadzamy nowe zmienne xi’ i xi’’ i zamieniamy wystąpienia xi na różnicę xi’-xi’’.
4. Gdy zmienna xi musi być większa od pewnej wartości di: xi ≥ di, wprowadzamy zmienną xi’, taką, że xi′ = xi − di
Podobnie w przypadku mniejszości (w miejsce większości): xi′ = di − xi
5. Dla ujednolicenia przyjmujemy, że mamy do czynienia wyłącznie z mniejszością nieostrą (<=). Gdy wśród warunków jest użyty znak większości – zamieniamy go na mniejszość mnożąc obie strony przez -1
6. Gdy mamy warunek równości – zamieniamy go na dwa warunki nierówności nieostrej (dotyczy to także =0). Przedstawmy zagadnienie z wcześniej rozważanego przykładu w postaci wektorowej:
Przedstawmy zagadnienie z wcześniej rozważanego przykładu w postaci wektorowej:
(1) x1>=2*x2 – 100 == -x1+2*x2 <= 100 == -1*x1 + 2*x2 <= 100
(2) x1<=0.5*x2 – 10 == x1 - 0.5*x2 <= - 10 == 1*x1 - 0.5*x2 = - 10
A*[x] = [b]
z = <c * x>
A = [ [-1,2], [1,-0.5], ]
b = [100, -10]
c = [3,4]
W postaci standardowej:
(1) -1*x1 + 2*x2 <= 100 == -1*x1 + 2*x2 + 1 * x3 = 100
(2) 1*x1 - 0.5*x2 = - 10 == 1*x1 - 0.5*x2 + 1 * x4 = - 10
czyli:
-1*x1 + 2*x2 + 1*x3 + 0*x4= 100
1*x1 - 0.5*x2 + 0*x3 + 1*x4 = - 10
x1>=0, x2>=0,x3>=0>,x4>=0
z = x1+x2 →max
A=[ [-1,2,1,0],
A=[ [-1,2,1,0],
[1,-0.5,0,1]]
b=[100,-10]
c=[3,4]
Możemy przejrzeć wszystkie wierzchołki i (jak poprzednio) znaleźć rozwiązanie dla (x1=20,x2=60,x3=0,x4=0)
Podstawy
Aby zrozumieć algorytm Simplex, rozwiązujący zagadnienia programowania liniowego – musimy wprowadzić kilka prostych definicji i spostrzeżeń (lematów). Wiele z opisów i implementacji algorytmu simplex – jest trudnych do zrozumienia, gdyż brakuje takich prostych objaśnień. Albo też – wręcz przeciwnie – objaśnienia są obszerne i z wykorzystaniem bardziej ogólnych definicji matematycznych (formalnie wprowadzone zbiory wypukłe i ekstrema).
(1). Podzbiór zdefiniowany przez ograniczenia nazywamy dopuszczalnym. Każdy element tego zbioru nazywa się rozwiązaniem dopuszczalnym.
(2). Rozwiązanie dopuszczalne x, dla którego funkcja celu f(x) osiąga minimum (maksimum) nazywamy rozwiązaniem optymalnym.
(3). Ograniczenia definiują wielościan w przestrzeni n wymiarowej (gdzie n to ilość zmiennych). Wielościan ten nazywamy „wielościanem ograniczeń”.
(4). W wielościanie ograniczeń wierzchołek to jedyny punkt wspólny (rozwiązanie dopuszczalne) dla kilku (więcej niż 1) ograniczeń (zapisanych w postaci równań). Inaczej mówiąc wierzchołek to punkt wspólny dla kilku krawędzi.
(5). Dwa wierzchołki są sąsiadami, jeśli różnią się wartością jednej zmiennej. Taka zmienna może służyć do poszukiwania lepszych rozwiązań (posuwając się od wierzchołka do jego sąsiada poprzez zmianę wartości tej zmiennej). Wtedy nazywamy ją „uwolnioną”.
(6). Jeśli funkcja celu osiąga minimum (lub maksimum), to musi ona osiągać to ekstremum w wierzchołku wielościanu. Ponieważ funkcja celu jest zależnością liniową, mając dowolne rozwiązanie poza wierzchołkiem – możemy odpowiednio zwiększać lub zmniejszać wartość zmiennych, powodując zmianę wartości funkcji celu na bardziej zbliżoną do optymalnej. Takiej możliwości nie ma tylko w wierzchołku.
Bardziej ścisłe wprowadzenie tych pojęć: http://smurf.mimuw.edu.pl/node/1121
Algorytm opisany przez tego samego autora: http://smurf.mimuw.edu.pl/node/1122
Idea rozwiązania
Algorytm simplex w największym skrócie: zamiast przeglądać wszystkie wierzchołki wielościanu, wybierz jeden i posuwaj się wzdłuż krawędzi do sąsiadów – póki możesz poprawić w ten sposób wartość funkcji celu.
1. Nierówności możemy zamienić na równania – odpowiednio dodając (<) lub odejmując (>) dodatkową („sztuczną”) zmienną. Taki zbiór równań jest liniowo niezależny (żadne z nich nie wynika z pozostałych). Na naszym przykładzie:
x1*4 + x2*2 - x3 = 250
x1*3 + x2*6 - x4 = 300
x1*12 + x2*15 → max
x1, x2, x3, x4 >= 0
2. Ten układ równań ma trywialne rozwiązanie przy założeniu, że x1=x2=0. Otrzymamy dokładnie jedno rozwiązanie: x3=-250 i x4=-300. Zgodnie z definicją takie rozwiązanie będzie wierzchołkiem wielościanu wielowymiarowego zdefiniowanego przez równania liniowe ograniczeń. Zmienne niezerowe nazwiemy bazą, a ich zbiór – zbiorem bazowym.
3. Algorytm Simplex polega na przeglądaniu sąsiednich wierzchołków wielościanu ograniczeń w poszukiwaniu rozwiązania lepszego (dającego lepszy wynik funkcji celu). Gdy taki znajdziemy – dokonujemy przesunięcia do następnego wierzchołka i znów przeszukujemy sąsiednie.
Ten skrótowy opis zostanie uzupełniony i wyjaśniony poniżej.
Algorytm Simplex
Istnieje kilka wariantów algorytmu Simplex. W tym tekście opiszemy najczęściej spotykany – oparty o rozwiązania bazowe, z wykorzystaniem zmiennych luzu (swobodnych).
Jeśli mamy:
A - macierz ograniczeń o wymiarach (m,n);
b – wektor wyrazów wolnych o wymiarze m;
c – wektor definiujący funkcję celu o wymiarze n;
x – wektor n zmiennych decyzyjnych (rozszerzony o zmienne swobodne/luzu), przyjmujących wartości nieujemne.
Bazą nazywamy macierz (oznaczaną jako B) składającą się m liniowo niezależnych kolumn macierzy A. Kolumny wchodzące w skład B nazywamy kolumnami bazowymi (pozostałe kolumny macierzy A nazywa się kolumnami niebazowymi). Zmienne związane z kolumnami bazowymi nazywamy zmiennymi bazowymi zaś nazywamy pozostałe niebazowymi. Rozwiązanie bazowe uzyskujemy, ustawiając wartość 0 (zero) dla wszystkich zmiennych niebazowych.
Jeżeli układ równań AxT=bT posiada rozwiązania oraz (n>m), to posiada skończoną liczbę rozwiązań bazowych – jest ich co najwyżej:
Każdemu rozwiązaniu bazowemu odpowiada wierzchołek wielokąta ograniczeń. Dowód znajdziesz na stronie: http://smurf.mimuw.edu.pl/node/1121
Przeglądanie wierzchołków wielomianu sprowadza się więc do zmiany rozwiązania bazowego poprzez „wymianę” zmiennych bazowych. Jedna zmienna wchodzi do bazy, a inna z niej wychodzi. Taka wymiana następuje wyłącznie wtedy, gdy dzięki niej udaje się zwiększyć wartość funkcji celu.
Pierwsze rozwiązanie bazowe możemy znaleźć dzięki wykorzystaniu „zmiennych swobodnych” (luzu). Zakładamy, że tylko one będą różne od zera. Ponieważ w każdym ograniczeniu mamy inną zmienną swobodną (odpowiedni współczynnik a[i]==1) – przy wyzerowaniu pozostałych zmiennych, przyjmą one odpowiednie wartości z b. W naszym przykładzie:
A=[ [-1,2,1,0], [1,-0.5,0,1]]
b=[100,-10]
c=[3,4,0,0]
Mamy zatem
x1=x2=0
x3 = 100
x4=-10
z=0
Zauważmy, że dzięki wykorzystaniu zmiennych swobodnych, punkt zerowy w pierwotnym układzie współrzędnych (x1,x2) stał się rozwiązaniem dopuszczalnym.
Jeśli początek układu współrzędnych jest rozwiązaniem dopuszczalnym, to jest także rozwiązaniem optymalnym wtedy i tylko wtedy, gdy wszystkie współczynniki funkcji celu [c] są mniejsze lub równe zeru (przy założeniu, że funkcja celu ma być maksymalizowana). Uzasadnienie jest proste: skoro wszystkie wartości zmiennych decyzyjnych X są większe lub równe zeru, to jeśli i-ty element [c] (c[i]) jest większy od zera, zwiększenie współrzędnej i (x[i]>0) powoduje zwiększenie funkcji celu.
Ponieważ algorytm z wykorzystaniem rozwiązania bazowego jest równoważny z algorytmem „geometrycznym” – ta reguła nadal obowiązuje. W przekształceniach dążymy do tego, by wszystkie elementy c były mniejsze lub równe zeru (przy szukaniu maksimum).
Do przekształceń wykorzystujemy metodę eliminacji Jordana-Gaussa. W tym celu tworzy się tablicę Simplex – dodając do A kolumnę b oraz wiersz c (uzupełniony zerem do rozmiaru n+1).
Tablica Simplex:
A | b
------
c | 0
W naszym przykładzie pierwsze rozwiązanie bazowe byłoby optymalne, gdyby lista c zawierała tylko ujemne elementy. Tak oczywiście nie jest (mamy [3,4]). Wybieramy kolumnę i o wartości dodatniej (max(c[i]) i wprowadzamy ją do bazy – eliminując współczynniki w tej kolumnie (sprowadzone do zera) – poza jednym – przy nowej zmiennej bazowej.
W wyniku przekształcenia jedna ze zmiennych bazowych x[j] zostanie usunięta z bazy (współczynnik c[j] zostanie wyzerowany, a inna x[i] znajdzie się w bazie (współczynnik a[i] otrzyma wartość 1). (Na temat wyboru wiersza i kolumn będzie jeszcze mowa poniżej).
Taką transformację możemy wykonać w następujący sposób:
1) dzielimy wybrany wiersz w przez wartość komórki tego wiersza z wybranej kolumny (i) (A[w][i]) – w ten sposób współczynnik a[i] otrzyma wartość 1);
2) odejmujemy ten wiersz od pozostałych po pomnożeniu przez wartość komórki wybranej kolumny zmienianego wiersza (dla wiersza u będzie to A[u][i]).
Ten sposób przekształcenia gwarantuje, że wcześniej wybrane do bazy kolumny nie zostaną zmienione – chyba, że zawierają 1 w wybranym aktualnie wierszu.
Przekształcamy w ten sposób tablicę simplex tak długo, aż wszystkie elementy c[i] będą mniejsze lub równe zeru, albo nie uda się znaleźć przekształcenia dającego wzrost funkcji celu (wtedy przyjmujemy, że zadanie nie ma rozwiązania).
Na naszym przykładzie (ostatni wiersz zawiera funkcję celu):
S=[
[-1, 2, 1, 0, 100],
[1, -0.5, 0, 1, - 10],
[3,4,0,0,0]
]
Redukcję tabeli przedstawimy wykorzystując napisany powyżej program eliminacji Jordana-Gaussa:
1. W kolumnie 0 mamy wartość już 1 w wierszu 1 (nie musimy wykonywać działania 1)). Pozostałe elementy redukujemy do zera dodając wiersz :
dodaj_wiersz(S,0,1,-S[0][0])
dodaj_wiersz(S,2,1,-S[2][0])
2. W kolumnie 1 sprowadzamy do 1 element wiersza 0, dzieląc go przez jego wartość (S[0][1]=1.5).
Podobnie jak poprzednio odejmujemy wiersz zerowy od pozostałych, mnożąc go przez element eliminowany (z kolumny 1):
mnoz_wiersz(S,0,1/S[0][1])
dodaj_wiersz(S,1,0,-S[1][1])
dodaj_wiersz(S,2,0,-S[2][1])
Wynik naszych działań:
Ostatnia kolumna zawiera wynik – wartości zmiennych x oraz funkcji celu:
0.00, 1.00, 0.67, 0.67, 60.00
1.00, 0.00, 0.33, 1.33, 20.00
0.00, 0.00, -3.67, -6.67, -300.00
Uwaga! Wartości zmiennych w ostatniej kolumnie dotyczą zmiennych bazowych. Jeśli zmienna decyzyjna nie jest obecna w bazie - oznacza to, że w rozwiązaniu jej wartość wynosi zero (0).
Trzeba jeszcze ustalić sposób wyboru wiersza i kolumny do wprowadzenia do bazy. Zgodnie z tak zwaną „regułą Blanda” ( https://www.mimuw.edu.pl/~oskar/lecture_13.pdf ), można przyjąć, przy wyborze kolumny wybieramy pierwszą z lewej o dodatnim współczynniku c, a następnie wiersz, dla którego najmniejszy jest iloraz wyrazu wolnego (b[i]) przez element z wybranej kolumny (dla kolumny k będzie to najmniejsza spośród b[i]/a[k][i] (oczywiście pod warunkiem, że mianownik jest dodatni).
Rozważmy inny przykład:
2x1-x2<=4
x1+2x2<=9
-x1+x2<=3
z=2x1+5x2→max
rysunek dzięki https://www.matemaks.pl/program-do-rysowania-wykresow-funkcji.html
A = [[2, -1], [1, 2],[-1,1]]
b = [4, 9, 3]
c = [2,5]
S = [[2, -1,1,0,0,4], [1, 2,0,1,0,9],[-1,1,0,0,1,3],[2,5,0,0,0,0]]
print('tablica Simplex:')
druk_tabeli(S)
print('wybrany wiersz 0 kolumna 0:')
mnoz_wiersz(S,0,1/S[0][0])
dodaj_wiersz(S,1,0,-S[1][0])
dodaj_wiersz(S,2,0,-S[2][0])
dodaj_wiersz(S,3,0,-S[3][0])
druk_tabeli(S)
print('wybrany wiersz 1 kolumna 1:')
mnoz_wiersz(S,1,1/S[1][1])
dodaj_wiersz(S,0,1,-S[0][1])
dodaj_wiersz(S,2,1,-S[2][1])
dodaj_wiersz(S,3,1,-S[3][1])
druk_tabeli(S)
print('wybrany wiersz 2 kolumna 2:')
mnoz_wiersz(S, 2, 1/S[2][2])
dodaj_wiersz(S, 0, 2, -S[0][2])
dodaj_wiersz(S, 1, 2, -S[1][2])
dodaj_wiersz(S, 3, 2, -S[3][2])
druk_tabeli(S)
rozwiązanie:
tablica Simplex:
2.00, -1.00, 1.00, 0.00, 0.00, 4.00
1.00, 2.00, 0.00, 1.00, 0.00, 9.00
-1.00, 1.00, 0.00, 0.00, 1.00, 3.00
2.00, 5.00, 0.00, 0.00, 0.00, 0.00
wybrany wiersz 0 kolumna 0:
1.00, -0.50, 0.50, 0.00, 0.00, 2.00
0.00, 2.50, -0.50, 1.00, 0.00, 7.00
0.00, 0.50, 0.50, 0.00, 1.00, 5.00
0.00, 6.00, -1.00, 0.00, 0.00, -4.00
wybrany wiersz 1 kolumna 1:
1.00, 0.00, 0.40, 0.20, 0.00, 3.40
0.00, 1.00, -0.20, 0.40, 0.00, 2.80
0.00, 0.00, 0.60, -0.20, 1.00, 3.60
0.00, 0.00, 0.20, -2.40, 0.00, -20.80
wybrany wiersz 2 kolumna 2:
1.00, 0.00, 0.00, 0.33, -0.67, 1.00
0.00, 1.00, 0.00, 0.33, 0.33, 4.00
0.00, 0.00, 1.00, -0.33, 1.67, 6.00
0.00, 0.00, 0.00, -2.33, -0.33, -22.00
x1=1,x2=4
z = 22
Ten sam problem można rozwiązać przy pomocy arkusza Excel:
Przykładowa implementacja
Istnieje wiele opisów algorytmu i jego implementacji. Na przykład zwięzła implementacja w Pythonie: https://github.com/j2kun/ opisana w tekście: https://jeremykun.com/2014/12/01/linear-programming-and-the-simplex-algorithm/.
W jego analizie przyda się słowniczek:
- Zmienne decyzyjne - decision variables
- Funkcja celu - objective function
- Ograniczenia - constraints
- Zmienne ograniczeń - variable bounds
- zmienne swobodne (zmienna swobodna, zmienna luzu) - slack variables
- sąsiad – neighbor
- iloczyn skalarny - dot product
- analiza wrażliwości (sensitivity analysis)
- rozwiązanie (solution)
- rozwiązanie wierzchołkowe (cornerpoint solution)
- dopuszczalne rozwiązanie wierzchołkowe (feasible cornerpoint solution)
- sąsiadujące rozwiązania wierzchołkowe (adjacent cornerpoint solutions)
- stopnie swobody (degrees of freedom, df)
- test minimalnej proporcji (minimum ratio test)
Główna procedura simplex(c, A, b):
# Utwórz tabelę Simplex.
# Znajdź dodatni indeks ostatniego wiersza i zwiększ odpowiednią zmienną (dodając ją do bazy) na tyle, aby inna zmienna znalazła się w bazie zerowej (usuwając ją z bazy).
# Powtarzaj krok 2, aż ostatni wiersz będzie niedodatni.
# Wypisz ostatnią kolumnę.
def simplex(c, A, b):
tableau = initialTableau(c, A, b)
while canImprove(tableau):
pivot = findPivotIndex(tableau)
pivotAbout(tableau, pivot)
return tableau, objectiveValue(tableau)
Funkcja initialTableau tylko tworzy tabelę Simplex. Dodaje do wierszy A odpowiedni wyraz wolny z b. W ostatnim wierszu wstawia wektor c uzupełniony zerem.
def initialTableau(c, A, b):
tableau = [row[:] + [x] for row, x in zip(A, b)]
tableau.append([ci for ci in c] + [0])
return tableau
Funkcja canImprove() sprawdza, czy w ostatnim wierszu znajduje się nieujemny wpis:
def canImprove(tableau):
lastRow = tableau[-1]
return any(x > 0 for x in lastRow[:-1])
Funkcja findPivotIndex() szuka dodatniego elementu w ostatnim wierszu (zawierającym c), a następnie wiersza w wybranej kolumnie o minimalnym ilorazie:
def findPivotIndex(tableau):
# wybór elementu ostatniego wiersza, dla którego x>0
column_choices = [(i,x) for (i,x) in enumerate(tableau[-1][:-1]) if x > 0]
column = min(column_choices, key=lambda a: a[1])[0]
# sprawdzenie, czy rozwiązanie nie ograniczone (unbounded)
if all(row[column] <= 0 for row in tableau):
raise Exception('Linear program is unbounded.')
# sprawdzenie braku zdegenerowania: więcej niż jeden minimalny iloraz
quotients = [(i, r[-1] / r[column])
for i,r in enumerate(tableau[:-1]) if r[column] > 0]
if moreThanOneMin(quotients):
raise Exception('Linear program is degenerate.')
# wybór indeksu wiersza o minimalnym ilorazie
row = min(quotients, key=lambda x: x[1])[0]
return row, column
Funkcja dla pierwszej tabeli zwraca parę (row=1, column=0).
Następnie dokonywana jest zamiana – przy użyciu funkcji pivotAbout. Jej implementacja:
def pivotAbout(tableau, pivot):
i,j = pivot
pivotDenom = tableau[i][j]
tableau[i] = [x / pivotDenom for x in tableau[i]]
for k,row in enumerate(tableau):
if k != i:
pivotRowMultiple = [y * tableau[k][j] for y in tableau[i]]
tableau[k] = [x - y for x,y in zip(tableau[k], pivotRowMultiple)]
Główny program dla naszego przykładu:
if __name__ == "__main__":
b = [4, 9, 3]
c = [2, 5]
A = [[2, -1], [1, 2], [-1, 1]]
# add slack variables by hand
A[0] += [1, 0, 0]
A[1] += [0, 1, 0]
A[2] += [0, 0, 1]
c += [0, 0, 0]
t, v = simplex(c, A, b)
print("wynik:")
print("tabela simplex=")
for w in t:
print(', '.join('{:0.2f}'.format(x) for x in w))
print("wartość funkcji celu=")
print(v)
Wynik:
tabela simplex=
1.00, 0.00, 0.00, 0.33, -0.67, 1.00
0.00, 1.00, 0.00, 0.33, 0.33, 4.00
0.00, 0.00, 1.00, -0.33, 1.67, 6.00
0.00, 0.00, 0.00, -2.33, -0.33, -22.00
wartość funkcji celu=
22.0
Analiza działania algorytmu
Dla tablicy z jedną zmienną decyzyjną x1 i jedną zmienną luzu (x2) wartość funkcji celu będzie wynosić (x1/x1 – z dzielenia wiersza przez x1, a następnie odejmowanie wiersza):
z = 0-b1*c1*x1/x1
czyli (zgodnie z oczekiwaniem):
z=-b1*c1
Przykład:
| Tablica 1 | |||
| x1 | s1 | b | |
| 0 | 1,00 | 1,00 | 5,00 |
| c | 1,00 | 0,00 | 0,00 |
| Wiersz 0 podzielony przez a[0][0] – czyli 1 | |||
| 0 | 1,00 | 1,00 | 5,00 |
| Tablica 2 | |||
| 0 | 1,00 | 1,00 | 5,00 |
| c | 0,00 | -1,00 | -5,00 |
Zauważmy, że jeśli c1 byłoby <0 – zadanie nie miałoby rozwiązania dla liczb dodatnich.
Weźmy teraz pod uwagę dowolną tablicę Simplex w której została do zredukowania jedna kolumna ze zmienną decyzyjną. Na przykład odpowiadająca nierówności 2*x3<=3, oraz czynnikowi x3*4 w funkcji celu (kolumna x3, wiersz 2):
| Tablica 1 | |||||||
| x1 | x2 | x3 | s1 | s2 | s3 | b | |
| 0 | 2,50 | 0,00 | 2,00 | 1,00 | 0,50 | 0,00 | 8,50 |
| 1 | 0,50 | 1,00 | 0,00 | 0,00 | 0,50 | 0,00 | 4,50 |
| 2 | 0,00 | 0,00 | 2,00 | 0,00 | 0,00 | 1,00 | 3,00 |
| 3 | -0,50 | 0,00 | 4,00 | 0,00 | -2,50 | 0,00 | -22,50 |
| Wiersz 2 podzielony przez a[2][2] – czyli 2 | |||||||
| 2 | 0 | 0 | 1 | 0 | 0 | 0,5 | 1,5 |
| Tablica 2 | |||||||
| 0 | 2,50 | 0,00 | 0,00 | 1,00 | 0,50 | -1,00 | 5,50 |
| 1 | 0,50 | 1,00 | 0,00 | 0,00 | 0,50 | 0,00 | 4,50 |
| 2 | 0,00 | 0,00 | 1,00 | 0,00 | 0,00 | 0,50 | 1,50 |
| 3 | -0,50 | 0,00 | 0,00 | 0,00 | -2,50 | -2,00 | -28,50 |
Wykonanie redukcji zmienia wynik funkcji celu o b[2] podzielone przez x3[2] i pomnożone przez c z kolumny x3 (c[2]). Czyli najpierw wyliczamy ile co najwyżej może wynosić x3, a następnie odejmowana jest ta wartość od wyniku funkcji celu (przy liczeniu maksimum wynik jest uzyskiwany ze znakiem minus), po przemnożeniu przez odpowiedni współczynnik (c[2] – czyli 4).
Czyli redukcja działa dokładnie tak, jakbyśmy to zrobili bez automatu. Tak samo algorytm Simplex zadziałałby, gdyby dodać kolumnę z jedną wartością dla dowolnej wielkości tablicy.
Zastanówmy się na koniec – co się stanie, jeśli dodana kolumna x3 będzie zawierać wartości różne od zera 0 w więcej niż jednym wierszu. Prześledźmy zmiany tablicy od samego początku:
| Tablica 1 | ||||||||
| x1 | x2 | x3 | s1 | s2 | S3 | b | min. dla X1 | |
| 0 | 2,00 | -1,00 | 0,00 | 1,00 | 0,00 | 0,00 | 4,00 | 2,00 |
| 1 | 1,00 | 2,00 | 0,00 | 0,00 | 1,00 | 0,00 | 9,00 | 9,00 |
| 2 | 0,00 | 0,00 | 3,00 | 0,00 | 0,00 | 1,00 | 6,00 | |
| s | 2,00 | 5,00 | 5,00 | 0,00 | 0,00 | 0,00 | 0,00 | |
| Wiersz 0 podzielony przez a[0][0] – czyli 2 | ||||||||
| 0 | 1,00 | -0,50 | 0,00 | 0,50 | 0,00 | 2,00 | ||
| Tablica 2 | dla x2 | |||||||
| 0 | 1,00 | -0,50 | 0,00 | 0,50 | 0,00 | 0,00 | 2,00 | |
| 1 | 0,00 | 2,50 | 0,00 | -0,50 | 1,00 | 0,00 | 7,00 | 2,80 |
| 2 | 0,00 | 0,00 | 3,00 | 0,00 | 0,00 | 1,00 | 6,00 | |
| s | 0,00 | 6,00 | 5,00 | -1,00 | 0,00 | 0,00 | -4,00 | |
| Wiersz 1 podzielony przez a[1][1] – czyli -2.5 | ||||||||
| 1 | 0,00 | 1,00 | 0,00 | -0,20 | 0,40 | 0,00 | 2,80 | |
| Tablica 3 | dla x3 | |||||||
| 0 | 1,00 | 0,00 | 0,00 | 0,40 | 0,20 | 0,00 | 3,40 | |
| 1 | 0,00 | 1,00 | 0,00 | -0,20 | 0,40 | 0,00 | 2,80 | |
| 2 | 0,00 | 0,00 | 3,00 | 0,00 | 0,00 | 1,00 | 6,00 | 2,00 |
| s | 0,00 | 0,00 | 5,00 | 0,20 | -2,40 | 0,00 | -20,80 | |
| Wiersz 0 podzielony przez a[2][2] – czyli 3 | ||||||||
| 2 | 0,00 | 0,00 | 1,00 | 0,00 | 0,00 | 0,33 | 2,00 | |
| Tablica 4 | dla s1 | |||||||
| 0 | 1,00 | 0,00 | 0,00 | 0,40 | 0,20 | 0,00 | 3,40 | 8,50 |
| 1 | 0,00 | 1,00 | 0,00 | -0,20 | 0,40 | 0,00 | 2,80 | |
| 2 | 0,00 | 0,00 | 1,00 | 0,00 | 0,00 | 0,33 | 2,00 | |
| s | 0,00 | 0,00 | 0,00 | 0,20 | -2,40 | -1,67 | -30,80 | |
| Wiersz 1 podzielony przez a[1][2] – czyli 0,4 | ||||||||
| 2 | 2,50 | 0,00 | 0,00 | 1,00 | 0,50 | 0,00 | 8,50 | |
| Tablica 5 | ||||||||
| 0 | 2,50 | 0,00 | 0,00 | 1,00 | 0,50 | 0,00 | 8,50 | |
| 1 | 0,50 | 1,00 | 0,00 | 0,00 | 0,50 | 0,00 | 4,50 | |
| 2 | 0,00 | 0,00 | 1,00 | 0,00 | 0,00 | 0,33 | 2,00 | |
| s | -0,50 | 0,00 | 0,00 | 0,00 | -2,50 | -1,67 | -32,50 | |
Baza dla tego przykładu zmienia się następująco (s1,s2,s3) → (x1,s2,s3)→(x1,x2,s3)→(x1,x2,x3)→(s1,x2,x3)
Zmienna x3 wchodzi do bazy w „Tablicy 4”. Do tego momentu kolumna x3 nie wpływa na resztę tablicy (poza oczywiście uwzględnieniem w wartości funkcji celu). Wtedy wyliczana jest wartość x3 przez podzielenie ograniczenia (b[2]) przez współczynnik (x3[2]).
Gdyby jednak w tablicy pojawiła się liczba 1 w polu x3[1] - wtedy w miejsce x1+2*x2<9 mielibyśmy x1+2*x2+x3<9. Wtedy przy redukcji kolumny x2 – odpowiadającej wierszowi z wstawioną jedynką – zostanie ona „przeliczona” na wartości 0,2 i 0,4 (Tablica 3, wiersz 0 i 1) – co w tablicy 4 skutkuje zmniejszeniem b[0] i b[1] w tablicy 4 (odpowiednio 2*0,2 oraz 2*0,4).
| Tablica 1 | ||||||||
| x1 | x2 | x3 | s1 | s2 | S3 | b | min. dla X1 | |
| 0 | 2,00 | -1,00 | 0,00 | 1,00 | 0,00 | 0,00 | 4,00 | 2,00 |
| 1 | 1,00 | 2,00 | 1,00 | 0,00 | 1,00 | 0,00 | 9,00 | 9,00 |
| 2 | 0,00 | 0,00 | 3,00 | 0,00 | 0,00 | 1,00 | 6,00 | |
| s | 2,00 | 5,00 | 5,00 | 0,00 | 0,00 | 0,00 | 0,00 | |
| Wiersz 0 podzielony przez a[0][0] – czyli 2 | ||||||||
| 0 | 1,00 | -0,50 | 0,00 | 0,50 | 0,00 | 0,00 | 2,00 | |
| Tablica 2 | dla x2 | |||||||
| 0 | 1,00 | -0,50 | 0,00 | 0,50 | 0,00 | 0,00 | 2,00 | |
| 1 | 0,00 | 2,50 | 1,00 | -0,50 | 1,00 | 0,00 | 7,00 | 2,80 |
| 2 | 0,00 | 0,00 | 3,00 | 0,00 | 0,00 | 1,00 | 6,00 | |
| s | 0,00 | 6,00 | 5,00 | -1,00 | 0,00 | 0,00 | -4,00 | |
| Wiersz 1 podzielony przez a[1][1] – czyli -2.5 | ||||||||
| 1 | 0,00 | 1,00 | 0,40 | -0,20 | 0,40 | 0,00 | 2,80 | |
| Tablica 3 | dla x3 | |||||||
| 0 | 1,00 | 0,00 | 0,20 | 0,40 | 0,20 | 0,00 | 3,40 | |
| 1 | 0,00 | 1,00 | 0,40 | -0,20 | 0,40 | 0,00 | 2,80 | |
| 2 | 0,00 | 0,00 | 3,00 | 0,00 | 0,00 | 1,00 | 6,00 | 2,00 |
| s | 0,00 | 0,00 | 2,60 | 0,20 | -2,40 | 0,00 | -20,80 | |
| Wiersz 0 podzielony przez a[2][2] – czyli 3 | ||||||||
| 2 | 0,00 | 0,00 | 1,00 | 0,00 | 0,00 | 0,33 | 2,00 | |
| Tablica 4 | dla s1 | |||||||
| 0 | 1,00 | 0,00 | 0,00 | 0,40 | 0,20 | -0,07 | 3,00 | 7,50 |
| 1 | 0,00 | 1,00 | 0,00 | -0,20 | 0,40 | -0,13 | 2,00 | |
| 2 | 0,00 | 0,00 | 1,00 | 0,00 | 0,00 | 0,33 | 2,00 | |
| s | 0,00 | 0,00 | 0,00 | 0,20 | -2,40 | -0,87 | -26,00 | |
| Wiersz 1 podzielony przez a[1][2] – czyli 0,4 | ||||||||
| 2 | 2,50 | 0,00 | 0,00 | 1,00 | 0,50 | -0,17 | 7,50 | |
| Tablica 5 | ||||||||
| 0 | 2,50 | 0,00 | 0,00 | 1,00 | 0,50 | -0,17 | 7,50 | |
| 1 | 0,50 | 1,00 | 0,00 | 0,00 | 0,50 | -0,17 | 3,50 | |
| 2 | 0,00 | 0,00 | 1,00 | 0,00 | 0,00 | 0,33 | 2,00 | |
| s | -0,50 | 0,00 | 0,00 | 0,00 | -2,50 | -0,83 | -27,50 | |
To zmniejszenie (b[0], b[1]) należy interpretować jako wyliczenie wpływu x3 na x1 i x2 we wspomnianej wyżej nierówności (wiersz 1). Jak to policzylibyśmy bez tablicy? Przyjmując x1+2*x2+x3 = 9 (wiersz 1) i x3=2 (6/2 - wiersz 2). Jeśli w ostatecznym wyniku x1=0, to x2=(9-2)/2 =3.5. Czyli dokładnie tyle, ile wylicza algorytm. Plik:Simplex3.ods
- ↑ https://www.snopes.com/fact-check/the-unsolvable-math-problem/
- ↑ Justyna Kosakowska i Piotr Malicki, „Badania operacyjne - programowanie liniowe” https://www.snopes.com/fact-check/the-unsolvable-math-problem/